What is adversarial machine learning?

If you work in computer security or machine learning, you have probably heard about adversarial attacks on machine learning models and the risks that they pose. If you don't, you might not be aware of something very interesting -- that the big fancy neural networks that companies like Google and Facebook use inside their products are actually quite easy to fool.

What do we mean by "easy to fool", exactly? We can make very small changes to something (like a photograph or an email), and cause a machine learning model to behave in very unexpected ways. These changes are so small that you probably wouldn't notice with your human eyes.

Here's an example from the original paper describing adversarial inputs by Christian Szegedy et al.¹:

In each of these examples, the left most photograph is the original. Next to it is a mostly gray image with some patterns. When you add the original image to the grayish one, you get the right most image, which is the adversarial input. Each of these six different photographs ends up getting classified as an ostrich after the transformation is applied. If you zoom in really far on the adversarial images, you'll notice that it's really hard to tell they have been perturbed. If you look at the praying mantis in particular, there are clearly visible striations in the background above its thorax, but an unsuspecting eye might mistake these for jpeg compression artifacts.

Here's a second example from the same paper:

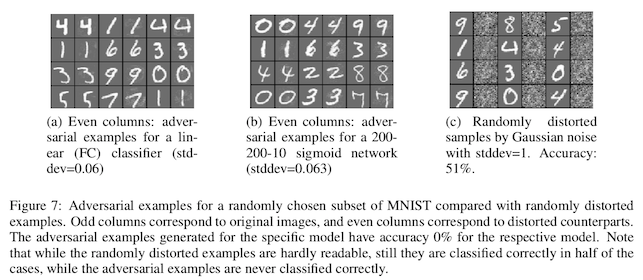
Again, in each of these examples, the applied changes are very small. Since the background is static its much easier to see them than it was in the natural photographs, but each numeral remains easy to read for a human. For a computer vision system, however, the accuracy in reading the numbers drops all the way down to 0%.

How does this work? The answer (given in this Goodfellow et al. paper²) is a little bit complicated, but basically it goes like this:

If you've taken a mathematics or a statistics class, you've probably learned about linear regression. The basic idea is that you have some number, maybe the size of a house in square feet, and you want to predict some other number, like the price of the house. So you write an equation that says

house price = something * number of square feet

You don't know what that "something" is, so you need to learn it from a sample of actual houses by dividing the total selling price by the house size. This is now a model, and that "something" you learned is your model parameter.

In this model, we only had one parameter, and it's pretty easy to understand the relationship between house price and square feet (as the house gets bigger, the price goes up). To make the model do something unexpected, you would need to change the input (the house size) by a lot -- maybe even making the square footage negative!

Now lets imagine that we added some more kinds of information to your model, like the number of bedrooms. You would probably expect that as the number of bedrooms increases, the price of the house also goes up, but this won't always be true. What if the house was 600 square feet, but also had four bedrooms? It's possible that this house would be much cheaper, since the bedrooms would be so small. It's also possible that there has never been a house that small with that many bedrooms in real life, and this can cause your model to do weird things.

In modern deep learning models, you might have one billion parameters, and it's an active area of research to understand what will happen when you change them. When you have this many parameters, tweaking just a few of them just a little bit can quickly put you in a space where no real life house has ever been. This is how adversarial inputs work -- they find a small change that you can apply to a real piece of data that moves it just far enough away from reality to cause the model to misbehave.

Here's a final example from the Goodfellow paper, just for fun:

This blog post first appeared on adversarial-designs.