Adversarial training: or, poisoning your model on purpose

So far, we have been looking at different ways adversarial machine learning can be applied to attack a machine learning model. We've seen different adversary goals, applied under different threat models, that resulted in giant sunglasses, weird t-shirts, and forehead stickers.

But what if you are the person with a model deployed into the wild, and you are worried about other people becoming adversaries and trying to make your model misbehave?

This isn't as far fetched as it might sound. In 2016, Microsoft launched a chat bot called Tay that learned in real time based on how people interacted with it. A small group of people started tweeting incendiary remarks at it, which encouraged the bot to repeat and expand on them, and the model was quickly taken offline.

A more recent example is OpenAI's chatgpt, and the large numbers of internet users who immediately tried to find ways to get around its built-in safety measures. You can see as an example this CNBC story about one particular prompt injection method that bypassed the safety filters. We showed in a recent blog post how you could also use chatgpt to write content for phishing attacks.

When models get deployed -- especially in a public setting -- it seems inevitable that some people will try to coerce it into misbehaving. If the attack method they are using involved adversarial machine learning, what can you do?

Well, you have a number of choices, which we'll elaborate on in future blog posts, but the first thing you might try is using adversarial attacks... on your own model!

The idea goes like this -- when you are training your model, you add adversarial noise to the inputs, so that the model sees data that look adversarial, but with the correct label. Because it saw these data during training time, it is less likely to be fooled by them during test time. This is called adversarial training, but you might think about this as the iocane powder approach.

via GIPHY

This method was used by Madry et al. in their 2018 paper, "Towards deep learning model resistant to adversarial attacks".¹ In their paper, they use two different adversarial attack methods -- the Fast Gradient Sign Method (FGSM) and Projected Gradient Descent (PGD) -- inside of their model training loop.

For each input data sample that goes through a forward pass of the network, these methods look at the gradient from the backwards pass with respect to the data. In FGSM, only the sign of the gradient is taken, and the input is updated by some small learning rate. In PGD, the magnitudes of the gradient are included in the update, but the update is also limited by the matrix norm. This inner loop is repeated for some number of iterations, say, between 5 and 20. Then, the input image with adversarial noise is fed to the model again, and this time the backwards pass is used to update the weights of the model to produce the correct label.

At the beginning of the training process, when the model doesn't really understand how to classify inputs, the gradients will be somewhat random and the adversarial attacks will mostly look like random noise. As the model learns from the data, the adversarial noise will start to converge on more successful attacks. Because of this dynamic where early inputs are noisy in an unhelpful way, some researchers let the model train without any adversarial inputs for a fixed number of epochs at the beginning. The practice of modifying a training process as the model learns -- usually to include easier inputs at the beginning and more diffult inputs at the end -- is known as curriculum learning.

Once you have your adversarially trained models, you can compare their performance to normal models. You can do this both on input images that have not been attacked ("clean" accuracy) and on images that have been modified by FGSM or PGD ("robust" accuracy). In the table below, this is also broken down by attack type: FGSM or PGD (attacks are on CIFAR10 in this table).

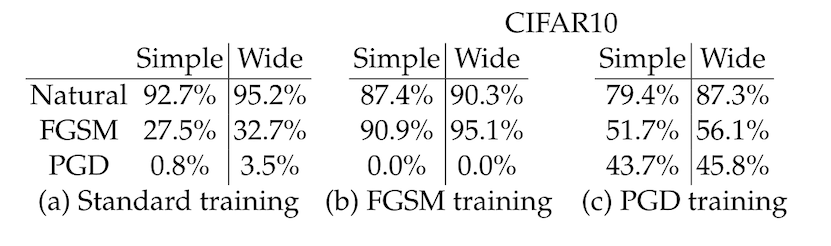
The first thing to note is that the "natural" training procedure produces a model which is very easily attacked -- PGD can reduce the accuracy from 95% to less than 5%! The second thing to note in this table is that the attacks from PGD are much more effective than the attacks from FGSM, on any model, adversarially trained or otherwise. Finally, and this is the main result for us here, adversarially trained models have much better robust accuracy than natural models under any adversarial attack.

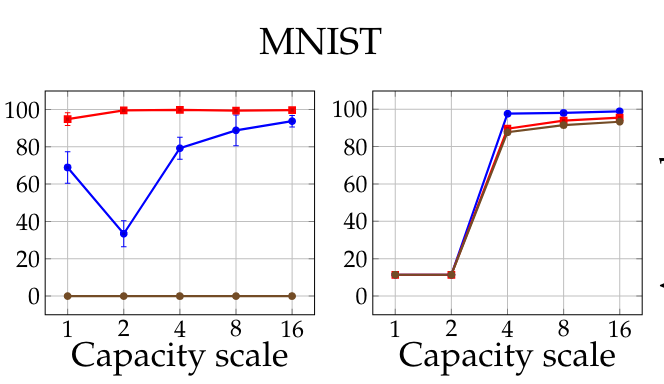
The authors note that it's important to have a high capacity model for this. If your model is not large enough, it will be overpowered by the adversarial inputs and experience mode collapse, which means it cannot do any better than predict the most common label present in the training data. This is shown in the figure below, which plots accuracy on MNIST as a function of training regime (blue for natural, brown for PGD, red for FGSM) and "capacity scale" on the x-axis, which involves increasing the width of the network by factors of 10.

One of the interesting affordances of this method is that the measured accuracy is provided in reference to bounds on the strength of the attack -- typicaly given as the maximum amount that any pixel can change, and some bound on the norm over the image. This translates directly to a "guarantee" about how much adversarial noise your model can see in its inputs and still operate safely. For example, you can demonstrate empirically that your model maintains some base level of performance (say, 80% top-1 accuracy) in the presence of an adversarial attack, as long as no pixel changes more than 4/255.

There are two downsides to the iocane powder approach. First, that inner adversarial attack loop makes model training quite a bit slower, so there is a non-trivial cost in both time and money spent on compute. Second, in some cases, you will see the accuracy of the model on unperturbed data get worse with adversarial training.

This second point is interesting, so we're going to go into a bit more detail here.

If you had been assuming that adversarial noise was a set of random pixel changes that happened to shift input data across a decision boundary, it's hard to explain why you would see clean test set accuracy degrade for robustly trained models. A follow-up paper in 2019 from the same lab attempts to explain why this happens.²

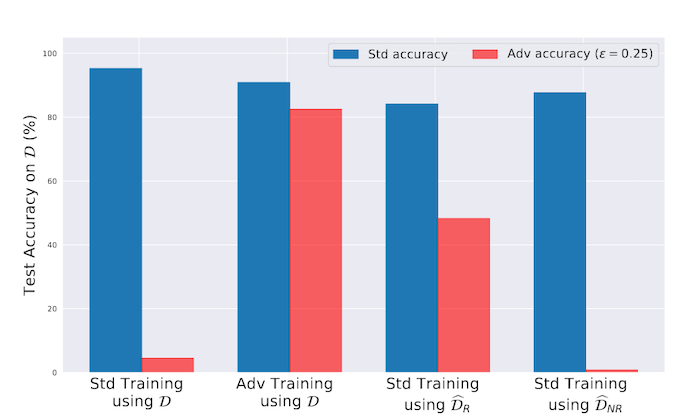
Briefly, the authors first replicate the finding that adversarially robust models show degraded performance against clean (i.e. non-attacked) examples. You can see in the figure below that a model trained the "standard" way (left-most bar) has high accuracy on clean data (Std), but low accuracy on adversarial inputs (Adv).

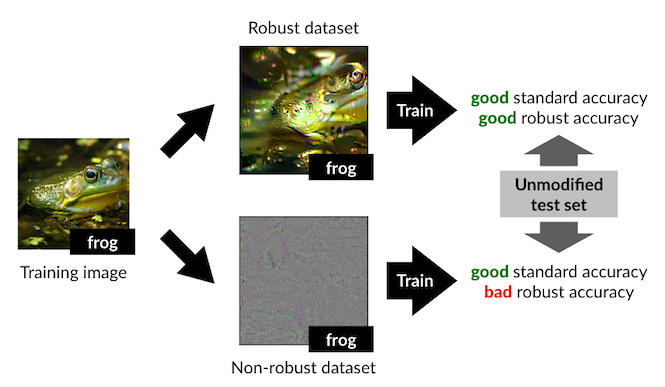
Then, they do something very interesting. They train a robust model on a dataset (here, CIFAR-10), then query the model for each input to find out which parts of the input image are important to the robust model. They call these the "robust" features. They subtract these from the input image, and call the leftover parts of the image the "non-robust" features. A schematic representation of this process is shown in the figure below:

A model trained the normal way on the robustified version of the input images ends up having pretty good clean accuracy, and somewhat good robust accuracy, indicating that the adversarial training process may be pushing the model to selective use robust features (third pair of bars from the left).

Here's the crazy part -- a model trained on just the leftover "not robust" noise does very well on clean inputs -- even better than the model trained on robust features! This is what the title of the paper "Adversarial examples are not bugs, they are features" is in reference to: these non-robust features, which look like noise to humans, are actually correlated with labels in the training data. It follows then that adversarial attacks also look like noise to humans, because what they are doing is applying the non-robust features from a different class to an image.

If you've been following along with the posts on this blog, this interpretation should sound familiar. We saw in "Natural adversarial examples", that image classification and object detection models tend to pay attention to image features that are only weakly correlated with labels -- in particular, these were colors, textures, and backgrounds. Generally speaking, this does not comport with the way humans recognize objects -- a boat is a boat whether it is in the ocean or not.

This raises the intriguing possibility that the "super-human" performance of some image classification models might only be statistical artifacts of the datasets they are evaluated on. This also has dramatic implications for AI safety, since you would want a self-driving car to recognize a stop sign no matter what is behind it, or a person wearing unusually-colored clothing.

Another way of looking at these results is that adversarial training has two other potential ancillary benefits: namely, better alignment with human judgment, and better robustness to distribution shifts in the data.

The same set of authors investigates this first possibility in another paper from 2019, where they train a series of robust models and visualize the importance of input pixels.³ In this first figure detail, we see on the MNIST numbers dataset that a non-robust model has activations in the image space that look a lot like noise, where a robust model has activations that are clearly aligned to the actual numerals:

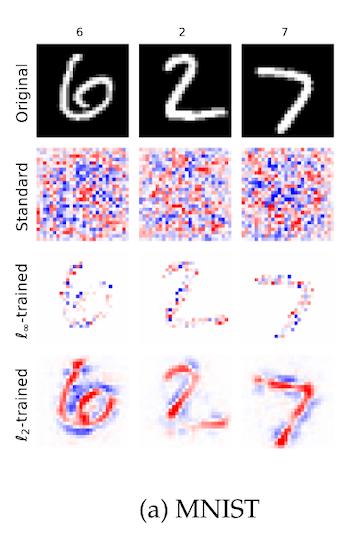
The authors call this "perceptual alignment". We can also see this on photgraphs of animals in imagenet, where the robust models are focusing on facial features and overall animal shape, in a way that the non-robust model is not:

This blog post about adversarial machine learning first appeared at adversarial-designs.

computer vision adversarial machine learning adversarial robustness